The Oscillation Principle

The Oscillation Principle begins with an unavoidable philosophical statement: any claim about existence is, by definition, philosophical. To exist is to move and to change; stillness carries no reality Nothing static can be real. Energy, motion, and wave are not separate things but one continuous act of persistence. The universe maintains continuity through cycles of compression and expansion. Compression keeps the rule intact by eliminating any configuration that cannot move or transform. From that act comes quantum differentiation, the first separation of coherent possibilities within the oscillatory field. Diversity follows as structure and geometry emerge from continuous motion. Over time these differentiated structures evolve into the ordered diversity observed in physical law. What begins as philosophy becomes physics. The mathematics of Entanglement Compression Theory show that only oscillation endures, and that from oscillation all structure flows.

1. First Measures: Planck Scales as Primitive Oscillation

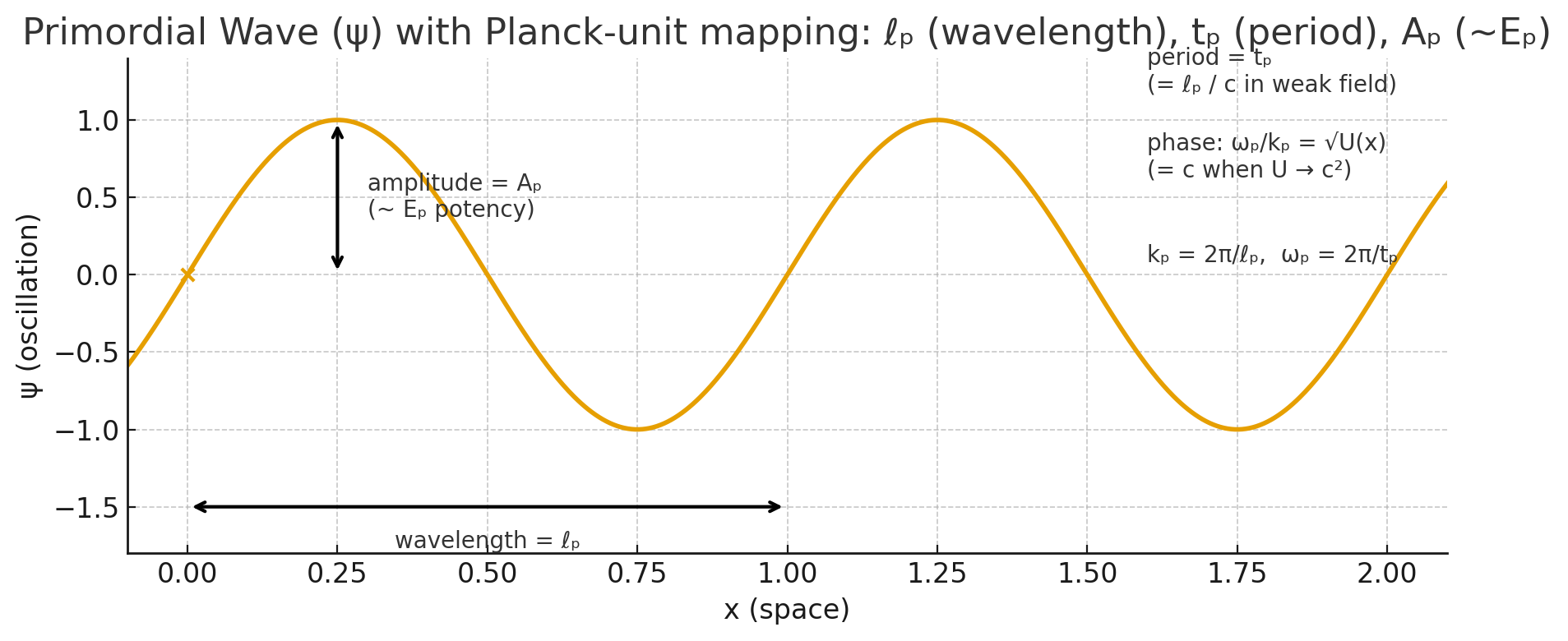
The Planck units record the first measurable rhythm of existence. They are not arbitrary numbers but the natural scales that appear when three universal constants are combined: Planck’s quantum constant (ħ), the speed of light (c), and Newton’s gravitational constant (G). When joined, they define distance, time, and energy at the point where all known forces converge:

ℓ_p = √(ħG/c³), t_p = √(ħG/c⁵), E_p = √(ħc⁵/G) .

Physically, these values describe the smallest interval through which causation can unfold without losing coherence. ℓ_p represents the minimal span of extension, roughly 10⁻³⁵ meters, beneath which geometry itself loses meaning. t_p is the corresponding tick of recurrence, the time an oscillation requires to complete its first causal cycle. E_p sets the amplitude of that cycle, the threshold energy that can curve space to its own wavelength. Together they define the primitive oscillation from which dimensional structure arises.

Historically, Planck introduced these scales in 1899 as mathematical curiosities, long before relativity or quantum mechanics were complete. They were later treated as boundary markers for spacetime, numbers describing where gravity and quantum theory might eventually meet. Entanglement Compression Theory reinterprets them as the first physical event. At ℓ_p, t_p, and E_p, the universe achieves its initial coherence: the smallest possible wavelength, period, and energy of motion. What classical physics calls constants are, in ECT, the preserved traces of that first oscillation, the moment when energy, time, and space became measurable as one act of compression.

ℓ_p marks minimal span, t_p marks recurrence, and E_p fixes the causal amplitude that initiates extension. Dimension is not a stage that precedes oscillation; dimension appears as the record of oscillation.

2. From Oscillation to Compression and Curvature

Oscillation alone creates rhythm but not structure. When oscillations interact, their phases align and interfere, forming what physics calls entanglement: a shared state of motion linking distant parts of the field. As entangled oscillations converge, their amplitudes reinforce each other and concentrate. This produces compression: the physical narrowing of wave density that induces measurable geometric deformation. .

Entanglement Compression Theory expresses this process through the Primordial Wave Equation (PWE), which governs the evolution of the Lawrence Universal Wave Function Ψ_L:

iħ ∂tΨ = (−αd Δ + V(x,t) + β ℂ[Ψ]) Ψ .

The term ℂ[Ψ] represents compression itself: a real, multiplicative operator that couples amplitude to curvature. It converts the density of motion into measurable geometry. The amplitude density ρ₁ = |Ψ|² defines local energy concentration, and its logarithmic gradients determine how that energy deforms the surrounding space through the symmetric compression tensor:

C(sym)μν = ∇μ∇ν(−lnερ₁) .

This tensor acts as a geometric stress field, bending space in proportion to how tightly oscillation is compressed. The effective metric is then

3. Local Transport: The Compression–Balance Law

Every oscillatory system maintains equilibrium between two opposing drives: dispersion, which spreads energy outward, and compression, which concentrates it. Entanglement Compression Theory expresses this equilibrium through a local invariant quantity,

U(x) = T(x) / C(x) .

Here T(x) represents the dispersive tension of the field, while C(x) measures its compressive curvature response. The ratio U(x) quantifies information transport through local geometry, defining the effective light speed.

c(x)² = U(x) .

When dispersion and compression balance perfectly, c(x) equals the universal constant c and geometry remains stable. Where the balance shifts, such as near strong density gradients or coherent compression zones, space deforms slightly and light paths record the strain of the underlying oscillation. The compression–balance law links the stability of geometry, the constancy of c, and the conservation of information as expressions of a single oscillatory equilibrium.

4. Probability as Coarse Measurement of Deterministic Division

When compression acts on an entangled system, it divides total energy deterministically among its available channels of resolution. Each channel receives a share proportional to the square of its amplitude in the full wave function, giving the measurable probability weights:

pi = ⟨Ψ, Pi Ψ⟩ .

Probability is not fundamental but reflects deterministic energy partition within a compressing field. Randomness appears only when measurement coarsens that division. What we interpret as chance is the visible trace of a deeper, deterministic redistribution of amplitude governed by compression geometry. The Born rule therefore arises not as an assumption but as the measurable surface of deterministic energy flow.

5. Core Propositions

The Oscillation Principle and its mathematical form in Entanglement Compression Theory reduce to a small set of physical statements. Each follows from the requirement that existence must move to persist, and that the flow of information shapes geometry itself:

• No static states: Persistence requires motion. Stillness carries no information and cannot endure. Oscillation is the minimum condition for reality.
• Dimension from motion: Span, recurrence, and amplitude are recorded as ℓ_p, t_p, and E_p, the Planck measures of the first oscillation. Dimension is not a background for motion but the record left by motion.
• Geometry from compression: Gradients of −lnρ₁ generate curvature through the symmetric compression tensor C^(sym)_μν. Geometry is the visible form of information density.
• Transport from balance: The invariant c(x)² = T/C links propagation stability to the balance between dispersion and compression, uniting optical and gravitational behavior in a single relation.
• Probability from partition: Born weights describe deterministic energy sharing across resolvable channels of compression, translating continuous dynamics into the statistics of observation.

6. Consequences and Limits

In uniform or smoothly varying domains, compression gradients vanish and the invariant U approaches c². Under these conditions, the Primordial Wave Equation reduces exactly to the linear Schrödinger form, and the effective metric g^eff_μν collapses to the background metric g_μν. Standard geodesic motion and all predictions of general relativity are recovered without modification.

Where gradients intensify, such as near gravitational boundaries, inside high-coherence cavities, or across large-scale density contrasts, finite compression leaves small, measurable traces. Phase-drift floors in interferometers, micro-arcsecond lensing asymmetries, and timing offsets that scale with κ̃L_*²∇²lnρ₁ are expected signatures. Each provides a falsifiable deviation predicted by compression geometry, marking the transition from smooth equilibrium to active spacetime formation.

7. Minimal Mathematical Skeleton

At its core, compression enters the Primordial Wave Equation through a real, multiplicative operator that captures how amplitude density responds to convergence. The functional form is logarithmic and regularized to preserve smooth behavior even in regions of extremely low density:

ℂ[Ψ](x) = −c₀ lnε(ρ₁(x)/ρ₀ + δ) .

Here ρ₁(x) = |Ψ|² is the local amplitude density, ρ₀ a reference scale, and small parameters ε and δ ensure analytic continuity at low amplitude. This regularization guarantees that ℂ[Ψ] remains differentiable and bounded, avoiding singularities that would otherwise arise in purely logarithmic compression. As β → 0, the operator vanishes and the Primordial Wave Equation reduces exactly to linear quantum mechanics, preserving all standard limits.

Under bounded time flux and Lipschitz continuity of ℂ[Ψ] in the Sobolev space H¹ for spatial dimensions d ≤ 3, global well-posedness of the system is established. Solutions exist, remain finite, and evolve continuously in time, showing that compression dynamics are mathematically complete and physically coherent.

8. Experimental Handles

Because compression modifies curvature and phase transport at measurable scales, Entanglement Compression Theory defines several concrete experimental signatures. Each effect is tied directly to the same parameters (κ̃, L_*, m_C, λ_C) that appear in the governing equations:

• Interferometry: Baseline-independent phase drift Δφ ≈ 10⁻¹⁸ rad·m⁻¹ from U(x) variability, observable as a fixed floor in high-precision Michelson or LIGO-class systems.
• Astrophysical lensing: Residual deflections δθ ≈ 1–3 μas across density contrasts in microlensing surveys, tracing curvature produced by compression gradients rather than mass alone.
• Solar-limb propagation: Fractional variation Δc/c ≈ (1–3)×10⁻⁶ along steep solar-edge gradients, offering a geometric test independent of plasma-dispersion effects.
• Cavity QED and BEC systems: Coherence-threshold shifts and dephasing-time changes correlated with controlled compression gradients in confined photon or condensate systems.

These observables span laboratory to cosmological scales and permit quantitative tests of the model parameters. A verified null result narrows those limits. A consistent deviation across independent domains would empirically confirm compression geometry as a real property of the universe.

9. Relation to the Main ECT Papers

The Oscillation Principle forms the causal base of the broader Entanglement Compression Theory framework. The Theory of Derived Probability and Entanglement Compression develops the link between deterministic energy division and the Born rule, defining probability as a coarse record of compression. Mathematical Foundations of Derived Probability and ECT establishes well-posedness, conservation, and transport in the Primordial Wave Equation. The Tensor Formalism and Curvature Geometry paper extends these results to full metric coupling, showing how compression fields generate curvature and reproduce the Einstein Field Equations in the weak-field limit.

These works connect directly: oscillation drives motion, compression yields curvature, and geometry preserves the resulting information flow. The sequence defines a single deterministic chain linking probability, structure, and spacetime.

10. Continuity and Closure

The Oscillation Principle completes the logic of Entanglement Compression Theory. It begins as a claim about existence: nothing can persist without motion, and it ends as a mathematical condition of the universe. Oscillation is not motion through space; it is the process by which space, time, and probability come into being. Compression gives that motion form. Differentiation gives it variety. Conservation allows it to last. All higher laws of physics, including curvature, energy flow, and coherence, follow from this single requirement that existence must keep moving to remain real.

In this framework, existence is defined by motion itself. Compression sets the limits, and oscillation sustains everything within them. The universe doesn’t expand into emptiness. It evolves within its own field of motion, where structure forms as motion stabilizes.

Source: Lawrence, W.A. (2025). The Oscillation Principle. Zenodo. https://doi.org/10.5281/zenodo.17058693

ECT Canonical Series:
Theory of Derived Probability and Entanglement Compression | Unified Derivation of Probability, Curvature, and Compression Geometry in Entangled Systems | Mathematical Foundations of Derived Probability and ECT